The Clock Synchronization and Ordering Problems
A single node system has no problem deciding what time it is and which order the events inside the system happened. The node has a timer, called clock, and any process that needs to make use of time makes a call to the operating system. If process \(a\) makes use of time before a second process \(b\), the time read by \(a\) will be smaller than the time read by \(b\). In a more formal way,
\[a \to b \implies T(a) < T(b)\]
This is a very natural condition. If something happens before another thing, it is expected that the time at the first thing occurred to be smaller. The operator \( \to \) is called happened-before, and it is defined as:
1. If \(a\) and \(b\) are events in the same process, and \(a\) occurs before \(b\), then \(a \to b\)
2. If event \(a\) is the sending of a message from a process, and event \(b\) is the receiving of the same message by another process, then \(a \to b \)
3. If \(a \to b\) and \(b \to c\), then \(a \to c\)
In a distributed system, however, the above condition is not so easy to maintain. We have multiple nodes. Each with its own clock. A clock is an electronic circuit present in the hardware made of a crystal that oscillates at a constant frequency. We call physical clocks this kind of clock that measures real-time. The problem in a distributed system is that there is no guarantee that the rate at which each one of the clocks oscillates will be the same, a phenomenon known as clock drift. This is the clock synchronization problem. Nodes can't agree on which time it is. Of course, measuring the real-time is important to many applications, so solutions to coordinate the clocks as NTP have been in use. However, even when using something like NTP and node's physical clock times becoming very close within a bounded range, it is still possible that an event happening before another to have a superior timestamp. There are many applications that it is important to have an agreement on the order of events. These applications cannot rely on physical clocks.
Lamport Clocks
In 1978, Leslie Lamport tackled this problem in the paper Time, Clocks, and the Ordering of Events in a Distributed System and presented a logical clock implementation built in a way to satisfy the above condition and it is able to make nodes agree on an order in which events occur.
A logical clock is just a counter that holds a number, called timestamp. This number has no relationship to physical time. Its only purpose is to capture the ordering of events. And in order to have this property, the clock needs to satisfy \(a \to b \implies T(a) < T(b) \) for any events \(a\) and \(a\). Lamport calls it Clock Condition. In other words, each node of a distributed system will have a clock (logical), that is just a counter; and all of the counters store numbers that are in agreement that if something happened the timestamp of this happening will be smaller than the next event.
It is not hard to come up with a counter the captures the condition. Let's break things into two parts: events happening inside a process and events happening between processes (messages exchange). If two events happen locally, a counter that increments its value every time an event satisfies the Clock Condition. For the second part, we have to satisfy the fact \(C_i(a) < C_j(b) \), where \(a\) is the event of sending a message at process \(i\) and event \(b\) is the receiving the same message at process \(j\); \(C_x\) is the value of the clock at process \(x\). Lamport proposes the sending of the timestamp together with the message and the receiver to update its counter to the greater value between its timestamp and the received one, upon receiving the message.
The Algorithm
Each node in a distributed system has a clock, which is a counter that stores the time t that the last event occurred. The counter starts at t = 0.
When an event occurs at the node, t is incremented, that is, t = t + 1.
When a node wants to send a message m to another node, t is incremented and it is sent together with the message, t = t + 1, then, send(m, t).
When a node receives a message, it updates its own clock with the maximum of its current time t and the time t_received that came with the message and adds one. That is, t = max(t, t_received) + 1.
Visualizing
I built a simple tool in Go that helps with defining the events in concurrent goroutines and visualizing the message flow and clock values. It is highly based on an implementation done by Michael Whittaker. You can plug your own example (like example3) and execute it by running go run cmd/* Example3 | ./plot.py .
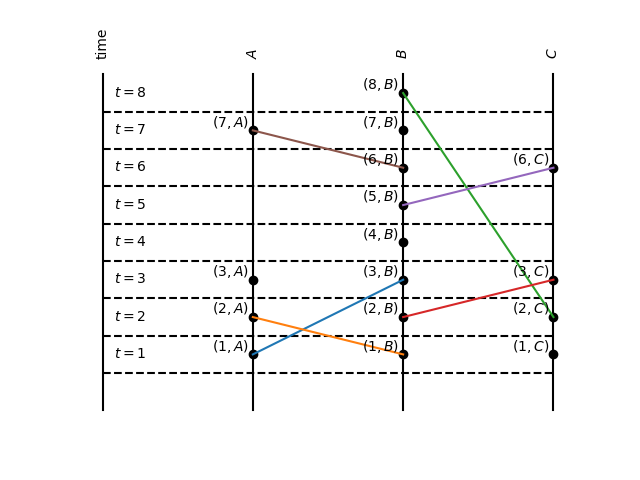
Every event has a mark on the timeline. A line in the figure is the connection between two events and it increases from the sender to the receiver.
It is very clear from the figure that the Clock Condition holds. Any pair of events that has a happened-before relation can be compared. For example, \( (1, A) \to (3, A)\); or \( (1, C) \to (8, B)\).
Does \( (1, A) \to (6, C)\)? Yes. According to the definition, \( (1, A) \) happened-before \( (6, C) \) by transitivity. There is a sequence of events from \( (1, A)\) to \( (6, C)\): \( (1, A), (3, B)\), \((4, B)\), \((5, B)\) and \((6, C)\). Be aware that for some pair of events we can't establish a happened-before relation according to our definition, for example, the pair \((3, A)\) and \((4, B)\). We say that these events are concurrent.
Total ordering
The usefulness of Lamport Clocks comes from the fact that it can be used to define a total order relation among all events in the system. In Lamport words,
We can use a system of clocks satisfying the Clock Condition to place a total ordering on the set of all system events. We simply order the events by the times at which they occur. To break ties, we use any arbitrary total ordering of the processes.
Being able to totally order the events can be very useful in implementing a distributed system. In fact, the reason for implementing a correct system of logical clocks is to obtain such a total ordering.
The use of Lamport Clocks and total ordering in a distributed system is what let us coordinate or synchronize events of multiple nodes in a way that every node agrees. It is a simple consensus algorithm.
Limitations
One limitation of Lamport Clocks is that the inverse of the Clock Condition does not hold:
\[T(a) < T(b) \implies a \to b \]
So it can't be used to determine if one event happens before the other given both timestamps. And also, it can't help us determine if to events are concurrent or not by comparing the timestamps only.
These limitations are overcome by Vector Clocks, the second kind of logical clock.
Vector Clocks
Vector Clocks is an improvement of Lamport Clocks, because it not only captures the happened-before (\( \to \)) relationship, that physical clocks do not have, but it also has the property of telling if events are concurrent or not, a property that Lamport Clocks don't have. Instead of holding only the timestamp of its own process, each clock holds a vector of timestamps, containing the timestamps of all processes. Apparently, it was first mentioned in 1986 at a paper called Highly-Available Distributed Services and
Fault-Tolerant Distributed Garbage Collection.
The Algorithm
Each node stores a vector of timestamps \(t = \langle t_1, t_2, \ldots, t_n \rangle \) of size n, where n is the number of nodes in the distributed systems. It is initialized at \( \langle 0, 0, \ldots, 0 \rangle \).
When an event occurs at a node i, it increments the ith entry of the t vector t[i] = t[i] + 1.
When a node i sends a message to another node, it increments the ith entry of the t vector t[i] = t[i] + 1 and attaches the vector with the message.
When a node i receives a message it updates its vector t using an element-wise maximum operation between its vector and the received vector t_received. Then, increments the ith entry of the t vector t[i] = t[i] + 1 .
Properties
Let's use the same tool to visualize the same sequence of events of the example before (this example can be found at example8.go).
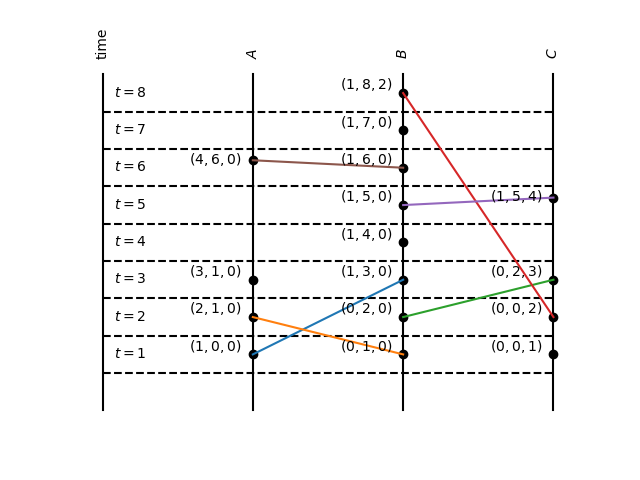
The first thing to observe is that we don't need to add the label of the process to uniquely identify a timestamp. A vector timestamp uniquely identifies an event. Second, we can see that the vector clock of an event is a counter of the number of events that has a happened-before relationship to the event. For example, the event \((3,1,0)\) informs that 2 events at A and 1 event at B happened-before it. And that is true, since the events \((1,0,0)\), \((0,1,0)\) and \((2,1,0)\) happened-before \((3,1,0)\). Another way of putting it: a vector timestamp of an event \(e\) represents a set of events, \(e\) and its causal dependencies: \( \{e\} \cup \{a \mid a \to e\} \).
Vector Clocks improves on Lamport Clocks on the fact that now you can compare event timestamps and decide which one happened before the other or if there are concurrent. We already said a vector timestamp uniquely identify an event, that is \( V(a) = V(b) \iff a = b \) for events \(a\) and \(b\). We can also compare if a vector timestamp is less (\(<\)) than another: for every element of the first vector it should be less or equal to the corresponding element of the second vector and the vectors can't be the same. The interesting fact is that \( V(a) < V(b) \iff a \to b \) for events \(a\) and \(b\). This means that given two vector clocks we can decide if one happened-before the other. If the events are not comparable by the equals (\(=\)) operator or the less (\(<\)) operator, we say that the events are concurrent. For example, we know that \((1,0, 0) \to (1, 5, 4)\) because \((1,0, 0) < (1, 5, 4)\). And we know that \((4,6,0)\) and \((0,0,1)\) are concurrent because they are not comparable.
Wrapping Up
This was a discussion on two popular kinds of logical clocks, their properties, and their implementations. Logical Clocks (not exactly the implementations provided above) are very important in distributed systems and very popular among databases for detecting conflicts of data versioning. Take a look at an excerpt from the Dynamo paper:
One can determine whether two versions of an object are on parallel branches or have a causal ordering, by examining their vector clocks. If the counters on the first object’s clock are less-than-or-equal to all of the nodes in the second clock, then the first is an ancestor of the second and can be forgotten. Otherwise, the two changes are considered to be in conflict and require reconciliation.
We can find examples on Riak KV that uses logical clocks to track the history of updates to values, and detect conflicting writes, and also on CockroachDB relies on hybrid logical clocks to provide serializability.
I hope you enjoyed the content. Consider following me on Twitter if that's the case. I write about databases internals while I learn more about it.
